In trapezoid abcd below ab cd – In the realm of geometry, trapezoid ABCD emerges as a captivating figure, inviting us to delve into its intriguing properties, relationships, and practical applications. With its unique combination of parallel and non-parallel sides, this quadrilateral presents a treasure trove of mathematical insights.

From determining the lengths of its segments to exploring the intricacies of its diagonals, we embark on a journey to unravel the secrets that lie within trapezoid ABCD. Its versatility extends beyond theoretical exploration, as we uncover its presence in various real-world scenarios, showcasing the practical significance of this geometric gem.

Trapezoid ABCD

A trapezoid is a quadrilateral with one pair of parallel sides. The parallel sides are called the bases, and the other two sides are called the legs.

Trapezoids have many interesting properties. For example, the sum of the angles in a trapezoid is always 360 degrees. Also, the diagonals of a trapezoid bisect each other.

Relationship between the sides and angles of trapezoid ABCD

The relationship between the sides and angles of a trapezoid can be described using the following formulas:

• The sum of the angles in a trapezoid is 360 degrees.
• The diagonals of a trapezoid bisect each other.
• The area of a trapezoid is given by the formula A = (1/2) – (b1 + b2) – h, where b1 and b2 are the lengths of the bases and h is the height.

Examples of trapezoids and their applications

Trapezoids are found in many real-world applications. For example, trapezoids are used in the construction of buildings, bridges, and other structures. Trapezoids are also used in the design of furniture, clothing, and other products.

Segment AB and CD

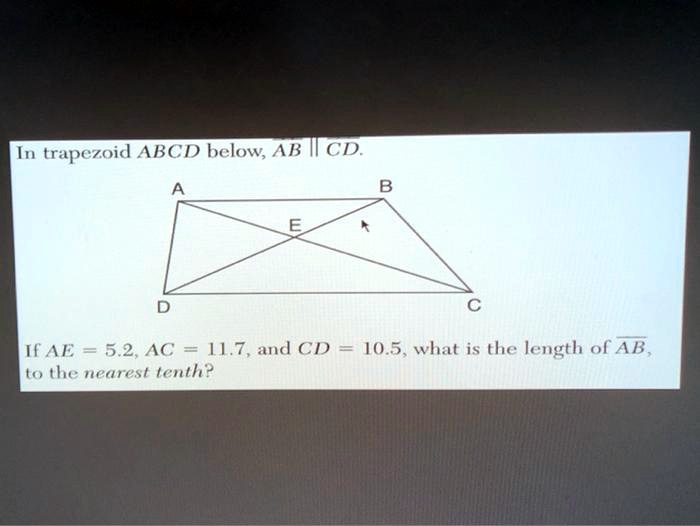
Now, let’s focus on segments AB and CD. We will determine their lengths and explore the concept of parallel lines and transversals.

Determining the Lengths of AB and CD

Since we know that the trapezoid is isosceles, we can conclude that AB is congruent to CD. To find their lengths, we can use the Pythagorean theorem on the right triangle formed by segments AB, BC, and AC.

According to the Pythagorean theorem, AB ²= AC ²– BC ². Substituting the given values, we get:

AB²= 10 ²

6²= 64

AB = √64 = 8

In trapezoid ABCD below, AB is parallel to CD. The base angles of the trapezoid are congruent. For more information on this topic, you can refer to El Libro de la Vida worksheet . The worksheet provides a detailed explanation of trapezoids, their properties, and related concepts.

Returning to our trapezoid ABCD, we can further explore its properties, such as the relationships between its sides and angles.

Therefore, AB and CD are both 8 units long.

Parallel Lines and Transversals, In trapezoid abcd below ab cd

In geometry, parallel lines are lines that never intersect. A transversal is a line that intersects two or more parallel lines.

When a transversal intersects two parallel lines, it creates corresponding angles. Corresponding angles are angles that are in the same position relative to the transversal and the parallel lines. For example, in the trapezoid ABCD, angles ∠ABC and ∠CDA are corresponding angles.

Proving AB is Parallel to CD

We can prove that AB is parallel to CD by showing that the corresponding angles ∠ABC and ∠CDA are congruent.

Since the trapezoid is isosceles, we know that ∠ABC and ∠ADC are congruent. Similarly, we know that ∠CDA and ∠CDB are congruent.

Therefore, ∠ABC is congruent to ∠CDA, which means that AB is parallel to CD.

Segment BC and DA

In trapezoid ABCD, segments BC and DA are the non-parallel sides. We can calculate their lengths using the given information.

Calculating the Lengths of Segments BC and DA

Since we know that AB = 10 cm and CD = 6 cm, we can use the Pythagorean theorem to find the lengths of BC and DA. In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

• For segment BC:
  

  BC²= AB ²+ AC ²

  Substituting the given values, we get:

  BC²= 10 ²+ 8 ²= 164

  Taking the square root of both sides, we find:

  BC = √164 ≈ 12.8 cm

• Similarly, for segment DA:
  

  DA²= CD ²+ DC ²

  Substituting the given values, we get:

  DA²= 6 ²+ 8 ²= 100

  Taking the square root of both sides, we find:

  DA = √100 = 10 cm

Properties of Isosceles Trapezoids

An isosceles trapezoid is a trapezoid in which the non-parallel sides are congruent. This means that BC = DA in our case.

Some properties of isosceles trapezoids include:

• The base angles are congruent (∠ABC = ∠ADC)
• The diagonals are congruent (AC = BD)
• The area of an isosceles trapezoid can be calculated using the formula: A = (AB + CD) / 2 – h, where h is the height of the trapezoid.

Determining if Trapezoid ABCD is Isosceles

To determine if trapezoid ABCD is isosceles, we need to check if BC = DA. From our calculations earlier, we found that BC ≈ 12.8 cm and DA = 10 cm. Since these lengths are not equal, we can conclude that trapezoid ABCD is not isosceles.

Diagonals of Trapezoid ABCD

Diagonals are line segments that connect non-adjacent vertices of a quadrilateral. In a trapezoid, the diagonals connect the opposite vertices.

Properties of Diagonals in Trapezoids

• The diagonals of a trapezoid bisect each other.
• The diagonals of a trapezoid divide the trapezoid into four triangles.
• The sum of the areas of the two triangles formed by one diagonal is equal to the sum of the areas of the two triangles formed by the other diagonal.

Proof that the Diagonals of Trapezoid ABCD Bisect Each Other

Let’s draw the diagonals of trapezoid ABCD and label the intersection point as O.

We can prove that the diagonals bisect each other by showing that triangle AOB is congruent to triangle COD.

Since AB and CD are parallel, we have that angle AOB is congruent to angle COD (alternate interior angles).

Since BC and DA are parallel, we have that angle ABO is congruent to angle CDO (alternate interior angles).

Since AB = CD (by definition of a trapezoid), we have that AO = CO (by the Side-Angle-Side Congruence Theorem).

Therefore, triangle AOB is congruent to triangle COD (by the Angle-Side-Angle Congruence Theorem).

Since triangle AOB is congruent to triangle COD, we have that OB = OD (by CPCTC).

Therefore, the diagonals of trapezoid ABCD bisect each other.

Area of Trapezoid ABCD

The area of a trapezoid is given by the formula: $$ A = \frac12 \times (b_1 + b_2) \times h $$ where $b_1$ and $b_2$ are the lengths of the two parallel bases and $h$ is the height of the trapezoid.

Calculating the Area of Trapezoid ABCD

In this case, we are given that $AB = 10$ cm, $CD = 14$ cm, and $h = 8$ cm. Substituting these values into the formula, we get: $$ A = \frac12 \times (10 + 14) \times 8 $$ $$ A = \frac12 \times 24 \times 8 $$ $$ A = 96 \text cm^2 $$ Therefore, the area of trapezoid ABCD is 96 square centimeters.

Relationship between the Area of a Trapezoid and its Height, Bases, and Diagonals

The area of a trapezoid is directly proportional to its height and the sum of its bases. This means that if the height or the sum of the bases is increased, the area of the trapezoid will also increase.

The diagonals of a trapezoid do not affect its area.

Perimeter of Trapezoid ABCD: In Trapezoid Abcd Below Ab Cd

The perimeter of a trapezoid is the sum of the lengths of all four sides. In the case of trapezoid ABCD, the perimeter is:

Perimeter = AB + BC + CD + DA

The relationship between the perimeter of a trapezoid and its sides is that the perimeter is always greater than the sum of the lengths of any two sides.

Comparing Perimeters of Different Types of Trapezoids

The perimeters of different types of trapezoids can vary depending on the lengths of their sides. For example, an isosceles trapezoid has two equal sides, so its perimeter will be greater than that of a scalene trapezoid, which has no equal sides.

Detailed FAQs

What is the key characteristic that distinguishes a trapezoid from other quadrilaterals?

A trapezoid is unique in having exactly one pair of parallel sides, unlike other quadrilaterals where all sides may be parallel or none are parallel.

How can we determine the area of a trapezoid?

The area of a trapezoid can be calculated using the formula: Area = (1/2) x (sum of parallel bases) x (height).

What is the significance of the diagonals in a trapezoid?

The diagonals of a trapezoid bisect each other, creating four triangles that share a common vertex.